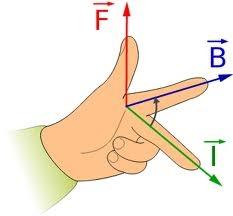
Co to jest efekt Halla?

Jeśli zapytasz osobę znającą fizykę napoziom tylko podstawowej wiedzy o tym, czym jest efekt Halla i gdzie jest stosowany, nie można uzyskać odpowiedzi. Co zaskakujące, w realiach współczesnego świata zdarza się to dość często. W rzeczywistości efekt Halla jest używany w wielu urządzeniach elektrycznych. Na przykład popularne niegdyś dyskietki komputerowe określiły początkową pozycję silnika za pomocą generatorów Halla. Odpowiednie czujniki "migrowały" do schematów nowoczesnych dysków CD (zarówno CD, jak i DVD). Ponadto, zakres zastosowania obejmuje nie tylko różne przyrządy pomiarowe, ale nawet generatory energii elektrycznej oparte na konwersji ciepła w strumień naładowanych cząstek pod wpływem działania pola magnetycznego (MHD).

Edwin Herbert Hall w 1879 roku, przeprowadzając eksperymenty zpłyta przewodząca, odkrył bezpodstawne, na pierwszy rzut oka, zjawisko pojawienia się potencjału (napięcia), w interakcji prądu elektrycznego i pola magnetycznego. Ale o wszystkim w porządku.

Zróbmy mały eksperyment myślowy: weź metalową płytkę i przepuść przez nią prąd elektryczny. Następnie umieszczamy go w zewnętrznym polu magnetycznym w taki sposób, że linie natężenia pola są zorientowane prostopadle do płaszczyzny płyty przewodzącej. W rezultacie na powierzchniach pojawia się różnica potencjałów (w kierunku prądu). To jest efekt Halla. Powodem jego pojawienia się są słynne siły Lorentza.

Istnieje sposób na określenie wartości uzyskanego napięcia (czasami nazywanego potencjałem Halla). Ogólne wyrażenie ma postać:

Uh = Eh * H,

gdzie H jest grubością płyty; Eh to siła pola zewnętrznego.

Ponieważ potencjał wynika zredystrybucja nośników ładunku w przewodniku, to jest ograniczona (proces nie trwa bezterminowo). Przesunięcie poprzeczne ładunków zatrzymuje się w momencie, gdy wartość siły Lorentza (F = q * v * B) jest zrównana z przeciwdziałaniem q * Eh (q jest ładunkiem).

Ponieważ gęstość prądu J równa się iloczynowi stężenia ładunków, ich prędkości i wartości jednostkowej q, czyli

J = n * q * v,

odpowiednio,

v = J / (q * n).

To implikuje (przez odniesienie wzoru do siły):

Eh = B * (J / (q * n)).

Połącz wszystkie powyższe i określ potencjał Halla przez wartość opłaty:

Uh = (J * B * H) / n * q).

Efekt Halla pozwala nam stwierdzić, że czasami wmetale obserwuje się nie przez elektrony, ale przez przewodność otworu. Na przykład jest to kadm, beryl i cynk. Studiując efekt Halla w półprzewodnikach, nikt nie wątpił, że nośniki ładunku są "dziurami". Jednak, jak już wskazano, dotyczy to metali. Uważano, że w rozkładzie ładunków (powstawanie potencjału Halla) wspólny wektor będzie tworzony przez elektrony (znak ujemny). Okazało się jednak, że elektrony w ogóle nie powstają w polu. W praktyce ta właściwość służy do określania gęstości nośników ładunku w materiale półprzewodnikowym.

Nie mniej znany jest kwantowy efekt Halla (1982rok). Jest to jedna z właściwości przewodności dwuwymiarowego gazu elektronowego (cząstki mogą poruszać się swobodnie tylko w dwóch kierunkach) w warunkach ultra niskich temperatur i wysokich zewnętrznych pól magnetycznych. Podczas badania tego efektu odkryto istnienie "frakcjonalności". Odcisnęło się wrażenie, że ładunek formowany jest nie przez pojedyncze nośniki (1 + 1 + 1), ale przez części składowe (1 + 1 + 0,5). Okazało się jednak, że żadne prawa nie są łamane. Zgodnie z zasadą Pauliego, wokół każdego elektronu w polu magnetycznym powstaje rodzaj wiru z kwantów samego przepływu. Wraz ze wzrostem natężenia pola powstaje sytuacja, w której przestaje być spełniona odpowiednia "jeden elektron = wir". Każda cząstka ma kilka kwantów strumienia magnetycznego. Te nowe cząsteczki są dokładnie przyczyną ułamkowego wyniku z efektem Halla.