Jak znaleźć powierzchnię sześcianu?

Kostka ma wiele interesujących elementów matematycznychwłaściwości i jest znany ludziom od czasów starożytnych. Przedstawiciele niektórych starożytnych szkół greckich wierzyli, że cząstki elementarne (atomy), które tworzą nasz świat, mają kształt sześcianu, a mistycy i ezoterykowie deifikowali tę figurę. A dzisiaj przedstawiciele parascience przypisują kostce niesamowite właściwości energetyczne.

Kostka jest idealną figurą, jedną z pięciu brył platońskich. Ciało platońskie jest

Poprawna wielościenna figura spełniająca trzy warunki:

1. Wszystkie jego krawędzie i twarze są równe.

2. Kąty między płaszczyznami są równe (w sześcianie kąty między ścianami są równe 90 stopni).

3. Wszystkie wierzchołki rysunku dotykają powierzchni opisanej kuli.

Dokładna ilość tych liczb zwanych grecki matematyk Theaetetus Aten, a uczeń Platona, Euklidesa w 13. księdze początku dał im szczegółowy opis matematyczny.

Starożytni Grecy skłonni przy pomocy ilościowejwartości opisujące strukturę naszego świata, nadały platońskim ciałom głębokie znaczenie sakralne. Wierzyli, że każda z postaci symbolizuje uniwersalne zasady: czworościan jest ogniem, sześcian jest ziemią, ośmiościan jest powietrzem, dwudziestościan jest wodą, dwunastościan jest eterem. Kula opisana wokół nich symbolizowała doskonałość, boską zasadę.

Tak więc sześcian, zwany także sześcianem (od greckiego. "hex" - 6), jest trójwymiarową regularną figurą geometryczną. Jest również nazywany regularnym pryzmatem czworokątnym lub prostokątnym równoległobokiem.

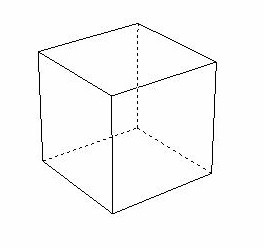
Kostka ma sześć twarzy, dwanaście krawędzi i osiemwierzchołki. Na tej figurze można wprowadzić inne regularne wielościany: czworościan (czworościan z twarzami w kształcie trójkątów), ośmiościan (ośmiościan) i dwudziestościan dwudziestoczęściowy.

Przekątna sześcianu jest segmentem łączącym dwa pionowo symetryczne wierzchołki. Znając długość krawędzi sześcianu a, można znaleźć długość przekątnej v: v = a^3.

W sześcianie, jak wspomniano powyżej, można wprowadzić kulę, której promień wpisanej sfery (oznaczonej przez r) jest równy połowie długości krawędzi: r = (1/2) a.

Jeśli sfera jest opisana wokół sześcianu, wówczas promień opisywanej kuli (oznaczamy ją przez R) będzie wynosił: R = (3/2) a.

Dość powszechne w problemach szkolnych jest pytanie: jak obliczyć obszar

powierzchnia sześcianu? To bardzo proste, to całkiem oczywiste, aby wyobrazić sobie sześcian. Powierzchnia sześcianu składa się z sześciu ścian w kształcie kwadratów. Dlatego, aby znaleźć powierzchnię sześcianu, musisz najpierw znaleźć obszar jednej z powierzchni i pomnożyć przez ich liczbę: S_n= 6a^2.

Podobnie do tego, jak znaleźliśmy pole powierzchni sześcianu, oblicz obszar jego bocznych ścian: S_b= 4a^2.

Z tej formuły jasno wynika, że ​​dwa przeciwległe boki sześcianu są podstawami, a pozostałe cztery są bocznymi powierzchniami.

Możesz znaleźć powierzchnię sześcianu i innesposób. Biorąc pod uwagę, że sześcian jest prostokątnym prostopadłościanem, można zastosować pojęcie trzech wymiarów przestrzennych. Oznacza to, że sześcian, będący figurą trójwymiarową, ma 3 parametry: długość (a), szerokość (b) i wysokość (c).

Za pomocą tych parametrów obliczyć powierzchnię całkowitej powierzchni sześcianu: S_n= 2 (ab + ac + bc).

Aby obliczyć powierzchnię bocznej powierzchni sześcianu, obwód podstawy musi być pomnożony przez wysokość: S_b= 2c (a + b).

Objętość sześcianu jest produktem trzech składników - wysokości, długości i szerokości:
V = abc lub trzy sąsiednie krawędzie: V = a^3.

</ p>